@第5章 召回之厚
双塔+ANN虽然在现在的召回中处于霸主地位,但也并非完美无缺。#card
对双塔来说,最大的问题就是用户和物料的特征交互得太晚了,这两部分在最后一层才通过点积产生交互。
如果能在网络计算前期就让它们产生交叉,模型的性能可能会有非常大的提升。
FM的成功已经说明了用户和物料的交叉是多么重要。
把双塔的检索过程放在树结构中 #card
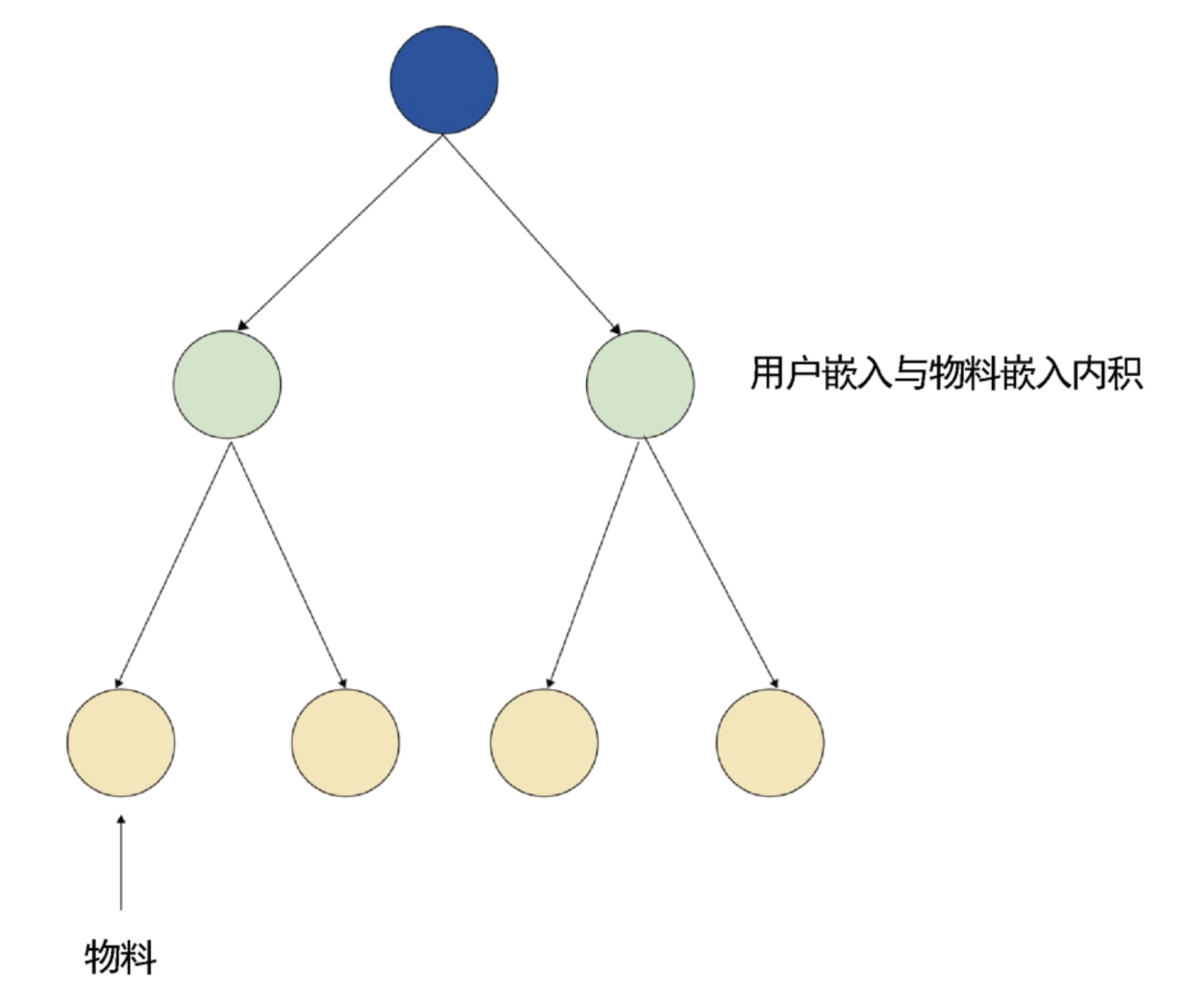
ANN的操作就是一个3层的树模型,同时把向量量化简化为k均值聚类,那么绿色节点就是k均值聚类的聚类中心。
所有物料都在叶子(黄色)节点上,只是通过量化把它们“捏”到绿色节点上。
此时只有绿色节点是实际运算的节点,选取哪个绿色节点的函数是一个计算用户喜好的函数,设为f。
在双塔中,这个函数的计算方式就是用户和物料输出嵌入的内积。
搜索的过程就是遍历所有的第2层节点,从中选出固定个,把下面的叶子节点全部纳入结果。
[[TDM]]
从上面的框架出发,能更加容易地理解TDM的原理。首先TDM继承了上面的形式,让物料都在叶子节点上。不过此时,由于不再使用ANN,上面3层的约束可以拿掉了,此时是一棵任意深度的树模型。#card
TDM中最重要的设定是除叶子节点外,父节点也有用户和物料交互的预估值,但这个值等于子节点中最大的值除以当前层的归一化系数。
这么说有点绕,换句话说就是子节点在该层中最大,那么父节点在上一层中也最大。
有了这样的设定,在第l层中找到Top-K个节点,在第l+1层中的Top-K一定都是上面那些的叶子节点。
这样的话,执行过程就是在每一层计算所有节点,排序后找到Top-K最大的节点(如果已经有一些叶子节点,就认为这部分已经找到了,要去掉,同时K的数值也要变化),然后继续往下搜索。
TDM检索过程的抽象图 #card
此时还在树模型的架构中,不过喜好函数变成了一个深度模型(非双塔,可以是MLP等结构)。
训练时如果用户的正样本是3号,那么模型就把3号当作正样本,而同时做负采样,在4、5、6号中可能采样出一个或多个当作负样本一起训练,令3号与用户交互的得分大于其他人与用户交互的得分。
再上一层,由于1号是3号的父节点,它也会被视为正样本,而此时2号成为负样本。
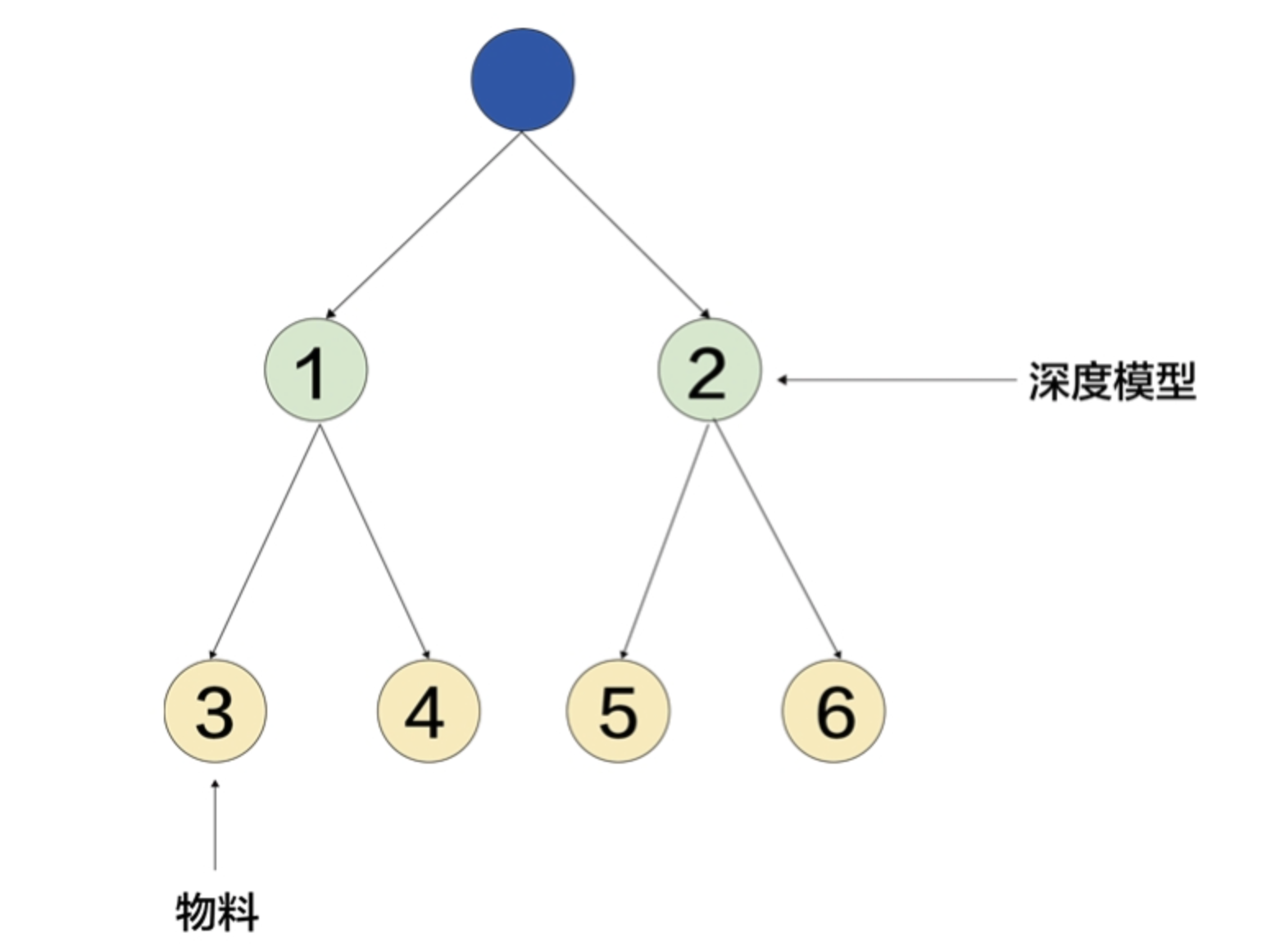
在树结构中的每一个节点上都有一个嵌入,那么实际搜索时,用户的信息可以和此节点的嵌入产生复杂运算,然后决定沿着哪些节点继续搜索。#card
在这里,复杂运算就可以不用双塔实现,而由MLP甚至包含注意力机制的模型实现,
这样就实现了我们喜好函数的计算在很早的阶段就引入用户和物料交叉信息的目标。
构造树模型的时候可以引入一些先验,#card
如同类别的物料大概率是相似的,那么可以初始化一棵树,让属于同一个父节点的所有叶子节点属于同一类别。
开始训练后,节点上的嵌入会慢慢变得成熟,此时可以根据这些嵌入重新聚类,让相近的叶子节点在一起,然后重复上述过程。
[[Deep Retrieval]]
- 再次对比TDM的实现和我们一开始提出的基准框架,可以发现TDM继承了大部分的设定,如物料是以叶子节点的形式存在的,而DR打破了这一设定,在DR中,#card
从上到下的一条路径代表一个物料。在树模型中,如果不把物料放在叶子节点上,就没有必要出现逐层增多的形式。
也就是说,既然已经让路径代表物料了,就没有必要每层节点都不一样,为简单起见,可以设定成一个方阵,有D层,每层有K个节点,这就是DR中的数据结构

+ 在第1层中,DR通过一个MLP+Softmax指出用户嵌入应该被分配在 **哪个节点** 上;到了第2层,还是用MLP来分配,不同的是,这里的输入是原始用户嵌入和上层所选节点嵌入的拼接,后面以此类推。
- 假设我们简化一下DR的形式,让物料的表示从根节点过来,经过每一个节点的嵌入的拼接,同时规定只要两个物料的最终嵌入不是完全一样的,就可以接受。这样会发生什么?#card
